MATEMATICAS
SEMANA 20
El día 6 de julio iniciaremos el tercer periodo con horario de lunes, con una reunión sincrónica a las 9:00 am se enviará el link 5 min antes de la reunión.
Marcar el segundo periodo Copiar temáticas e indicadores
TEMATICAS
PENSAMIENTO NUMERICO Y SISTEMAS NUMERICOS.
Números primos y compuestos.
Múltiplos y divisores de un numero.
MCM y MCD
PENSAMIENTO ESPACIAL Y SISTEMAS GEOMETRICOS
Polígonos irregulares y clasificación
PENSAMIENTO ALEATORIO Y SISTEMA DE DATOS.
Tablas y diagramas estadísticos Perímetro y área
INDICADORES
· Identifica números primos, compuestos y halla el máximo común divisor y el mínimo común múltiplo de dos o mas números.
Reconoce y construye polígonos regulares e irregulares y los diferencia según sus características.
NO SE DEBE ENVIAR ESTA ACTIVIDAD.
· SEMANA 11 abril 12 al 16 ( 5 HORAS DE CLASE )
PPLANO CARTESIANO y PAREJAS ORDENADAS (Trabajo 2 Horas) (Copie la teoría en el cuaderno)
Cuando relacionamos dos conjuntos, podemos armar parejas como ( 3 , 9 ) y ubicar estas parejas en un plano llamado cartesiano, donde hay coordenadas X en las horizontales y coordenadas Y en la verticales, y cada cuadro se denomina un cuadrante, así.
El primer número se ubica en el eje X y el segundo número en el eje Y.
ejemplo: ( 2 , 3 ) y se ubica la pareja donde se encuentren los dos puntos.
Cuando los números están debajo de la línea horizontal y al lado izquierdo, se escriben con un signo menos y serán números negativos ( - 3 , - 1 )
.
https://www.youtube.com/watch?v=kzOzYY-T-50
https://www.youtube.com/watch?v=QTrE4x5DPZ8
ACTIVIDAD
Copie la actividad y desarróllela en el cuaderno.
Ubique las parejas con un punto, una los puntos y descubra el dibujo de una hoja como la bandera de Canadá.
Miguel Ángel pintó la Capilla Sixtina en el siglo XVI
Para nombrar a los reyes:
Fernando II de Aragón se casó con Isabel I de Castilla
Para numerar los tomos o partes de algunos libros o películas:
Ayer vi en la televisión El padrino I
Para aniversarios, reuniones o festejos que se celebran periódicamente:
Se está organizando el IV certamen de fotografía juvenil
TABLA DE NÚMEROS ROMANOS
https://www.youtube.com/watch?v=GY4ITArm-9A
Fecha máxima de entrega jueves 16 de Abril
Escribir en asunto
Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha y actividad correspondiente.
Ejemplo… Asunto: Pérez Sergio 503 Matemáticas semana 12 plano romanos descomposición
501actividades2021@gmail.com
· 503actividades2021@gmail.com
· 504actividades2021@gmail.com
LA MULTIPLICACIÓN 2 HORAS copie la teoría, ejemplos y realice las actividades.
Multiplicación es una suma abreviada, donde se suma un número tantas veces como lo indique el otro por ejemplo: 45 X 3 = 45 + 45 + 45 =135
Términos de la multiplicación
Estos son términos y las partes de la multiplicación.
TABLAS DE MULTIPLICAR Repaso
Realizar la multiplicación del numero del lado por cada uno de los de arriba y completa el siguiente cuadro.
ACTIVIDAD
Realizar las siguientes multiplicaciones
2. Mandar un video de un minuto máximo, diciendo de forma rápida y con los ojos cerrados y de memoria las tablas del 9 y del 8. (Esta Actividad que se había anunciado repasar desde el primer periodo.)
PROPIEDADES DE LA MULTIPLICACIÓN (2 HORAS DE TRABAJO)
Estas son las propiedades: conmutativa, asociativa, modulativa y distributiva.
Propiedad distributiva:
La suma de dos números multiplicada por un tercer número es igual a la suma de cada sumando multiplicado por el tercer número.
Por ejemplo 4 x (6+3) = 4 x 6 + 4 x 3
- Propiedad conmutativa
El orden de los factores no altera el producto. Si se multiplican dos números, el producto es el mismo sin importar el orden Por ejemplo: 4 x 2 = 2 x 4
Propiedad asociativa
Cuando se multiplican tres o más números, el producto es el mismo sin importar como se agrupan los factores.Por ejemplo (2 x 3) x 4 = 2 x (3 x 4)
Propiedad modulativa
El producto de cualquier número natural por el número 1, el producto es el mismo. da como resultado el mismo número. Para la multiplicación, el módulo es el número 1.
ACTIVIDAD (1 HORA)
1. Completa. utilizando la propiedad distributiva.
4 x (2 + 5) = ( x -) + ( x ) =
8 x (10 + 7) = ( x ) + ( x ) .=
2.
Fecha máxima de entrega jueves 22 de Abril
Escribir en asunto
Asunto: Apellidos y nombres completos del estudiante, SEMANA seguido del área y fecha y actividad correspondiente.
Ejemplo… Asunto: Pérez Sergio 503 Matemáticas semana 14 MCM
501actividades2021@gmail.com
· 503actividades2021@gmail.com
· 504actividades2021@gmail.com
SEMANA 13 Abril 26 al 30
COPIE LA TEORIA Y EJEMPLOS, LUEGO VEA LOS VIDEOS EXPLICATIVOS. NO ENVIE AL CORREO
NÚMEROS PRIMOS Y COMPUESTOS
Múltiplos de un número.
Los múltiplos de un número son aquellos que se obtienen al multiplicar un numero por otro.
Para saber si un número es múltiplo de otro, se divide y el cociente es el múltiplo si el residuo de la división es 0.
Un múltiplo común es aquel que es múltiplo a la vez de dos o más números.
ejemplo:
Para hallar el mínimo común múltiplo de dos o más números debemos de descomponer el número en factores primos.
Por ejemplo: Descomponer 40 y 60 en sus factores primos
Por lo tanto 40 se descompone en: 2x2x2x5
Por lo tanto 60 se descompone en: 2x2x3x5
El mínimo común múltiplo (mcm) es el número más pequeño que es múltiplo de dos o más números.
Vamos a calcular el mínimo común múltiplo de 4 y 6. Para ello, escribimos los primeros múltiplos de 4 y de 6:
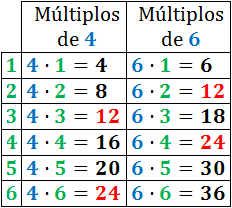
Entre los múltiplos de 4 y de 6, el número 12 es el múltiplo común mas pequeño entre ambos números.
Por tanto, el mínimo común múltiplo se escribe de la siguiente manera:
ADELANTE ACTIVIDADES ATRASADAS DURANTE ESTA SEMANA.
SEMANA 14 Mayo 3 al 7 ( 5 HORAS DE CLASE )
Vea el video explicativo
}
ACTIVIDAD NÚMEROS PRIMOS
https://www.youtube.com/wat
ch?v=c11n-QDzTGk&t=109s
ACTIVIDAD MULTIPLOS
Escribir en asunto
Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha y actividad correspondiente.
Ejemplo… Asunto: Pérez Sergio 503 Matemáticas semana 14 MCM
Tan pronto tenga el recibido del docente coloque el visto en la lista de chequeo.
501actividades2021@gmail.com
· 503actividades2021@gmail.com
· 504actividades2021@gmail.com
SEMANA 15 Mayo 3 al 7
Reflexión sobre nuestro país
Indague cuales son las cosas mas bellas que hacen de Colombia uno de los mejores países del mundo.
Vea el video Colombia es pasión y realice una reflexión del la importancia de amar a nuestra Colombia y la importancia del respeto y el amor por el otro y por lo público.
si desea no es obligatorio, puede enviar una pancarta sobre esa importancia.
Envíen lo realizado al siguiente correo de la personera del colegio
florecitagrande03@gmail.com
https://www.youtube.com/watch?v=fTRXDuEcBeQ
SEMANA 16 Mayo 18 al 21
Divisores de un número.
https://edu.gcfglobal.org/es/divisores-y-multiplos/
Los divisores de un número son aquellos que pueden dividir a otro y el residuo es cero.
Para saber si un número es divisor de otro, solo tienes que hacer la división y comprobar si el resto es cero.
Ejemplo
¿Cuáles son los divisores de 15? Son números entre los que podemos dividir el 15 siendo el residuo 0. Luego los divisores del 15 son el 1, el 3, el 5 y el 15.
Podemos saber fácilmente si un número es divisible por otro sin hacer la división, simplemente observando estas características:
- Los múltiplos de 2 terminan en 0, 2, 4, 6, 8. ejemplo 48 es par por tanto es divisible por 2.
- Es múltiplo de 3 si al sumar sus cifras dan como resultado un múltiplo de 3. ejemplo 72 7+2=9 nueve es múltiplo de 3 por tanto es divisible por 3.
s· - Un número es divisible entre 4 si el número formado por las dos últimas cifras es un múltiplo de 4 o cuando termina en doble cero. ejemplo: 3400 es divisible por 4 porque termina en doble cero.
- Los múltiplos de 5 terminan en 0 o en 5.Para determinar el MCD podemos determinar cuales números dividen de forma exacta cada número dado, luego miramos cual es el máximo número que se repite en ambos números.
Ejemplo calculemos los divisores de y :
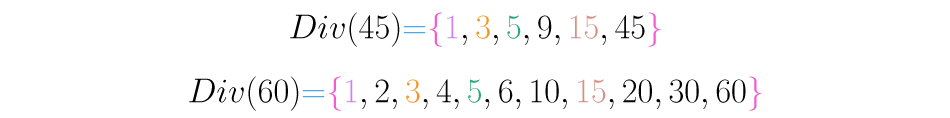
Observa que los números 3 y 15 son divisores comunes de 45 y 60. El mayor de estos números, es el máximo común divisor es decir 15.
entonces MCD(45,60)= 15
Un procedimiento más sencillo y corto para calcular el máximo común divisor de 300 y 198 es descomponerlos en factores primos.
Primero se debe realizar la descomposición de cada uno de los números hasta donde se pueda dividir ambos números: ejemplo
21 36 81 10 45 25 y 22 44 88
Fecha máxima de entrega jueves 20 de Mayo
Escribir en asunto
Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha y actividad correspondiente.
Ejemplo… Asunto: Pérez Sergio Mantematicas semana 15
Tan pronto tenga el recibido del docente coloque el visto en la lista de chequeo
501actividades2021@gmail.com
Los polígonos (2 horas de trabajo) Puede sacar fotocopias de las tablas y las figuras.
Partes del polígono
Lados: son los segmentos que forman la línea poligonal.
Vértices: son los puntos donde se unen los lados.
Ángulos: son las regiones del plano que delimitan dos lados.
Diagonal: es la recta que une dos vértices no consecutivos.
Centro: es el punto desde el que todos los ángulos y lados están a la misma distancia.
Radio: es el segmento que une el centro del polígono con cualquiera de sus vértices
Apotema: es el segmento que une el centro del polígono con el centro de cualquiera de sus lados.
Base: Es el lado inferior de un polígono. Normalmente es el lado donde se “apoya” la figura.
Clasificación de polígonos
· Clasificación de polígonos según sus lados:
o
o Cuadrilátero: 4 lados
o Pentágono: 5 lados
o Hexágono: 6 lados
o Heptágono: 7 lados
o Octógono: 8 lados
o Eneágono: 9 lados
o Decágono: 10 lados
o Endecágono: 11 lados
o Dodecágono: 12 lados
Clasificación de polígonos según sus lados y sus ángulos (1 hora de trabajo)
Polígonos regulares: es cuando un polígono tiene todos sus lados y ángulos iguales.
Polígonos irregulares: es cuando en un polígono hay uno o más lados y/o ángulos que no son iguales.
https://www.youtube.com/watch?v=AwdOocKn6m0
https://www.youtube.com/watch?v=E3i2ptq-G5w
El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono.
https://www.youtube.com/watch?v=wYNvY_bOGdc
ACTIVIDAD (dos horas de trabajo)
2.Calcular perímetro y área
-Calcular el área y el perímetro del siguiente trapecio:
-Calcular el área del siguiente polígono:
Fecha máxima de entrega jueves 27 de Mayo
Escribir en asunto
Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha y actividad correspondiente.
Ejemplo… Asunto: Pérez Sergio Mantematicas semana 17
Tan pronto tenga el recibido del docente coloque el visto en la lista de chequeo
501actividades2021@gmail.com
SEMANA 18 Mayo 31al 4 de Junio
Podemos mirando la gráfica, responder preguntas relacionadas con los resultados de la encuesta.
Ejemplo tenemos los siguientes datos
Primero reordena los datos del más pequeño al más grande.
por esto La mediana es 89. Me.= 89
Encontraremos la moda.
La moda es el número que aparece más veces. En este caso, 85 aparece dos veces y todos los otros números aparecen solo una vez. El número 85 es la moda.
La moda es 85. Mo.= 85
Encontremos la media. sumamos todos los datos y lo dividimos por el número total de datos
La media es 688,66 = 688,66
El rango es la diferencia entre el valor más alto y el valor más bajo en un conjunto de datos.
62 dato mas pequeño menos 105 dato mas grande
105-62= 43 este es el rango.
https://www.youtube.com/watch?v=0DA7Wtz1ddg
ACTIVIDAD
Fecha máxima de entrega jueves 3 de Junio
Escribir en asunto
Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha y actividad correspondiente.
Ejemplo… Asunto: Pérez Sergio Mantematicas semana 18
Tan pronto tenga el recibido del docente coloque el visto en la lista de chequeo
501actividades2021@gmail.com
Esta prueba estará disponible todo el día hasta las 11: 59 pm.
lea muy bien cada pregunta y conteste.
MUCHA SUERTE
El día 6 de julio iniciaremos el tercer periodo con horario de lunes, con una reunión sincrónica a las 9:00 am se enviará el link 5 min antes de la reunión.
.
https://elprofealejandro.jimdofree.com/matematicas/ https://www.aaamatematicas.com/grade5.htm#topic2
-------------------------------------------
SEMANA 1 ENERO 28 y 29
2. Organiza verticalmente los siguientes números en ese orden y resuelve las sumas:
a. 446.977 + 17 + 396 + 54.749
b. 38648 + 1897 + 49 + 532.797
3. Realiza las siguientes multiplicaciones
38648 65743 76543
x47 x 473 x6954
4. Realice las siguientes divisiones
a. 78658 dividido en 9
b. 54855 dividido en 15
5. Resuelve el problema:
6. Juan tiene cinco cajas de dulces, cada caja tiene 8325, su mamá le regala 83.99 dulces más. y su papa le quita 27542 ¿cuántos dulces tiene en total Juan?
7. Realice las operaciones con números decimales vistos el año pasado.
a. Suma 654,67 + 6746,9 + 654,876
b. Resta 6754,56 - 8258,6
c. Multiplicación 8875,7 x 674,78
d. 4763 dividido 35,3
8. Represente los siguientes fraccionarios
7/9 12/5 21/21
9. Realice las operaciones con fraccionarios
a. Suma 7/5 + 8/3 + 3/9
b. Resta 8/9 - 5/3
c. Multiplicación 12/4 x 8/6
d. División 9/8 dividid0 en 2/6
Realizar en el cuaderno de matemáticas y enviar foto al correo correspondiente según el curso.
SEMANA 2 FEBRERO 1 - 5
PRIMER PERIODO
INDICADORES
Se debe copiar la teoría de cada tema que se vea en el cuaderno siempre y realizar las actividades. Recuerde no debe sacar fotocopias.
DEFINICIÓN
Conjunto es una reunión objetos, que tienen una característica en común. Estos objetos pueden ser números, letras, días de la semana, países, alumnos, etc.; y se les conoce como "Elementos del Conjunto".
ACTIVIDAD
2. Representa el conjunto formado por los animales domésticos
DETERMINACIÓN DE CONJUNTOS
Por extensión: Cuando se nombra o se enumera cada uno de sus elementos.
P = {3; 4; 5; 6; 7}
Por comprensión: Cuando se nombra una característica común de un conjunto, utilizando para ello el símbolo x/x, que se lee: "x tal que x".
Extensión
P = {x/x las frutas amarillas} P = {x/x bananos, naranjas, mango}
P= {x/x el mango es una fruta amarilla}
Extensión
P = {x/x números naturales menores a 10.} P = {x/x 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
P ={x/x 7 es un número naturales menores a 10.}
N = { _________________________________________________ }
N = { América, Asia, África, Europa, Oceanía }
Q = { meses del año, cuya letra inicial es una vocal }
Q = { _________________________________________________ }
H = { _________________________________________________ }
H = { triángulo, cuadrado, círculo, rectángulo }
fecha máxima de entrega jueves 11 de febrero
Cuando envíen las evidencias al docente respectivo, se debe escribir en Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha de la actividad correspondiente.
Ejemplo… Asunto: Pérez Pepito Artes enero 25 al 29
correos según el curso.
· 502actividades2021@gmail.com
· 503actividades2021@gmail.com
· 504actividades2021@gmail.com
SEMANA 4 FEBRERO 15 - 19
Se debe copiar la teoría de cada tema que se vea en el cuaderno siempre y realizar las actividades. Recuerde no debe sacar fotocopias.
Los conjuntos pueden clasificarse en función de su número de elementos, en:
- Conjunto universal o referencial
Un conjunto es universal es cuando contiene todos los elementos según una característica, este se representa mediante la letra U en mayúsculas.
Por ejemplo, se puede definir como conjunto U, como el conjunto de todos los seres vivos del planeta. estos son, los animales, las plantas, los hongos y los microorganismos.
- Finito
Si tiene una cantidad que se pueda contar, Por ejemplo, el conjunto de frutas incluye todos los tipos de fruta que hay en el mundo, se podrían contar todos los tipos de fruta del mundo, por lo que es finito.
Cuando en un conjunto hay muchos elementos y no podemos escribir todos, se representan mediante tres puntos ‘...’
H = {números impares del 1001 al 1501} = {1001,1003,1005,...,1501} tiene un fin
- Infinito
Si tiene una cantidad de elementos que no tiene fin. Por ejemplo, el conjunto de todos los números pares.
{números pares} = {2,4,6,8,10...} En este caso los tres puntos indican muchos mas elementos.
- Vacío
No tiene ningún elemento. Se representa mediante el símbolo Ø o con dos claves vacías {}
- Unitario
Tiene un solo elemento
ACTIVIDAD
-Conjunto vacío -Conjunto unitario-Conjunto finito-Conjunto infinito
Relaciones entre conjuntos
En función de la relación entre dos conjuntos podemos encontrar.
- Conjuntos disjuntos o Independientes
Son conjuntos formados por elementos que no tienen ningún elemento en común
Por ejemplo, los conjuntos de frutas y de- animales son disjuntos, porque no hay ninguna fruta que sea un animal, ni ningún animal que sea una fruta:
- Conjuntos Iguales
Dos conjuntos son iguales en el caso de que contengan los mismos elementos.
Por ejemplo: A = {números impares del 1 al 15} y
B = {1,3,5,7,9,11,13,15}, entonces A = B.
- Conjuntos Diferentes
Si dos conjuntos no tienen los mismos elementos y, por tanto, no son iguales, se representa su desigualdad mediante el símbolo ‘≠’.
ejemplos
no tiene los mismos elementosC = {1,2,3} y D = {2,3,4}, por tanto C ≠ D. no tiene los mismos elementos
- Conjuntos equivalentes
Dos conjuntos son equivalentes si tienen la misma cantidad de elementos, pero sin que estos sean los mismos. Por ejemplo:
los dos conjuntos tienen la misma cantidad de elementos
Esto se representa de la siguiente manera: A ↔️ C.
A = {1,2,3} y B = {A,B,C}
(A) = 3, (B) = 3. Ambos conjuntos tienen tres elementos por esto son equivalentes.
Esto se representa de la siguiente manera: A ↔️ B.
Actividad
Según lo visto escriba dos ejemplos de cada relación entre conjuntos
-Disjuntos
- iguales
- diferentes
- equivalentes
fecha máxima de entrega jueves 18 de febrero
Cuando envíen las evidencias al docente respectivo, se debe escribir en Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha de la actividad correspondiente.
Ejemplo… Asunto: Pérez Pepito Artes febrero15 al 19
correos según el curso.
· 502actividades2021@gmail.com
Conjuntos subconjuntos
Se da cuando todos los elementos de un conjunto pertenecen al otro.
Por ejemplo, el conjunto de frutas rojas y el conjunto de frutas amarillas son subconjuntos del conjunto de frutas, puesto que todas las frutas rojas son frutas, y todas las frutas amarillas son frutas también. es decir, de un conjunto que pertenece a otro conjunto. usa el símbolo "⊆"
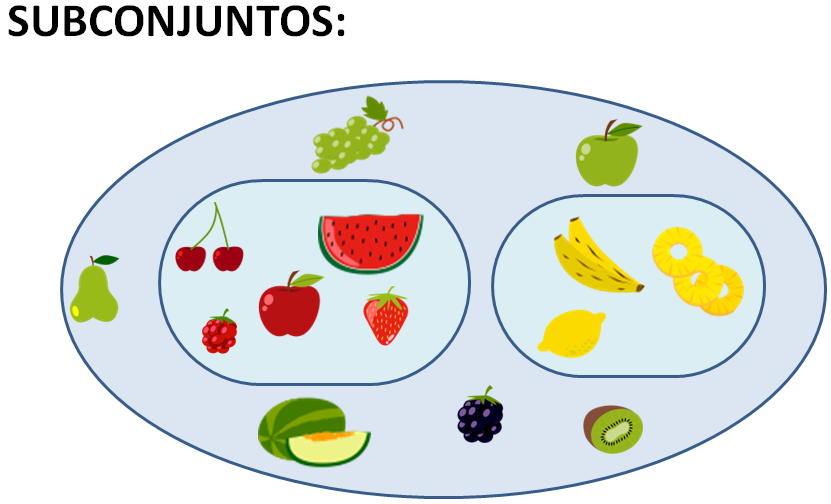R ⊆ F A ⊆ F
Unión de Conjuntos
La unión es aquel conjunto de una amplitud mayor que reúne a uno o más conjuntos. Para ello decimos que sus elementos reúnen las características de uno u otro conjunto.
Vamos a ver algunos ejemplos:
- Primero con elementos reales.
Por ejemplo, tenemos un conjunto de niñas, y otro conjunto de personas con gafas. Como hay niñas que tienen gafas, forman parte de la intersección de los dos conjuntos:
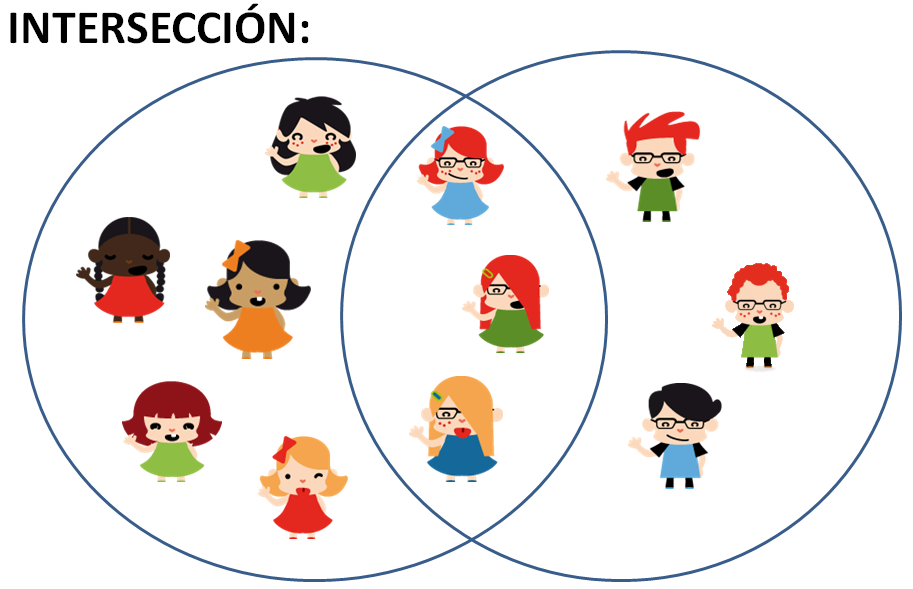
El símbolo de intersección es: ∩
https://www.smartick.es/blog/matematicas/recursos-didacticos/conjuntos-subconjuntos/
Son dos conjuntos cuyos elementos tienen la misma distancia entre ellos. Normalmente suelen ser de tipo numérico o alfabético.
Por ejemplo:
A = {1,2,3,4,...} y
B = {10,11,12,13,14,...}
Estos dos conjuntos son congruentes, dado que sus elementos tienen la misma distancia entre ellos, siendo una unidad de diferencia en cada eslabón de la secuencia.
Conjuntos no congruentes.
Los conjuntos no congruentes son aquellos en los que sus elementos no presentan la misma distancia entre ellos.
A = {1,2,3,4,5,...} y
B = {1,3,5,7,9,...}
En este caso se puede ver que los elementos de cada conjunto tienen distancias diferentes, siendo una distancia de una unidad en el conjunto A y una distancia de dos en el conjunto B. Por lo tanto, A y B no son conjuntos congruentes entre ellos.
Homogéneos
Todos los elementos del conjunto pertenecen a la misma categoría, es decir, son del mismo tipo: A = {1,2,3,4,5}
B ={azul,verde,amarillo,rojo}
C ={a,b,c,d,el}
Heterogéneos
Los elementos no tienen una característica clara en común, la inclusión de sus elementos parece ser debida al azar
A = {5, avión, X, caos}
Fecha máxima de entrega jueves 4 de marzo
Cuando envíen las evidencias al docente respectivo, se debe escribir en Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha de la actividad correspondiente.
Ejemplo… Asunto: Pérez Pepito Artes marzo 1-5
correos según el curso.
· 502actividades2021@gmail.com
Fecha máxima de entrega jueves 11 de marzo
Cuando envíen las evidencias al docente respectivo, se debe escribir en Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha de la actividad correspondiente.
Ejemplo… Asunto: Pérez Pepito Artes marzo 1-5
correos según el curso.
· 502actividades2021@gmail.com
El Punto: El punto es la intersección de dos líneas o la intersección de tres superficies.
La Línea: es una sucesión continua e indefinida de puntos. Una línea es la intersección de dos superficies.
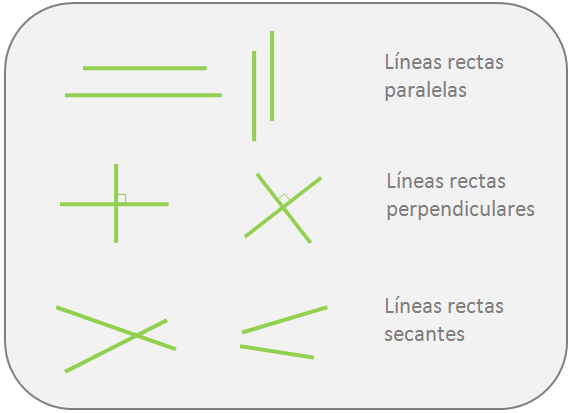
Tipos de líneas según la forma
Líneas rectas: Los puntos están trazados en una misma dirección. (sin curvas ni ángulos). Una recta puede tener dirección horizontal, vertical u oblicua.
Línea curva. Es una sucesión de infinitos puntos que cambian continuamente de dirección, sin formar ángulos.
Líneas Quebradas: Es la formada por varios segmentos de línea que tiene diferentes direcciones y forman ángulos cuando cambian de dirección.
Línea Mixta: es una línea que tiene partes rectas y curvas.
![[image]](https://i1.wp.com/www.webscolar.com/wp-content/uploads/2016/07/webscolar1493-6.jpg?resize=142%2C108 "webscolar1493-6.jpg")
Fecha máxima de entrega jueves 18 de marzo
Cuando envíen las evidencias al docente respectivo, se debe escribir en Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha de la actividad correspondiente.
Ejemplo… Asunto: Pérez Pepito Artes marzo 1-5
correos según el curso.
· 502actividades2021@gmail.com
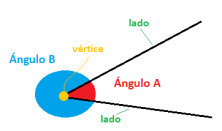
Es la porción comprendida entre dos semirrectas que tienen un origen común.
Partes nombre de un ángulo
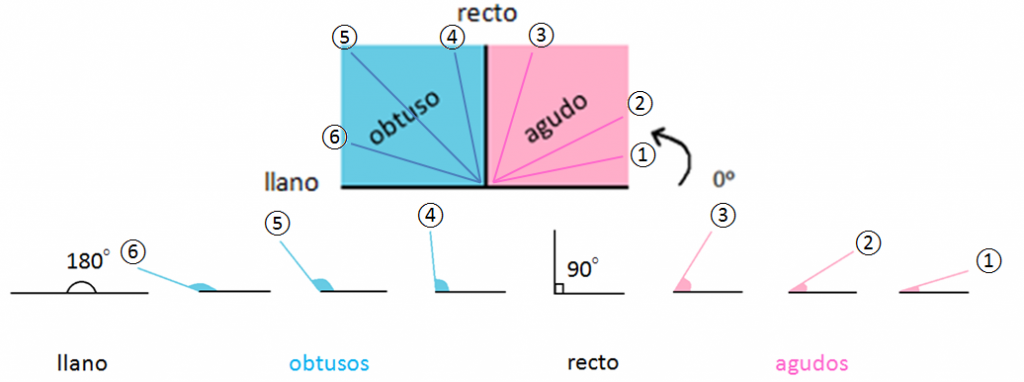
Tipos de ángulos
Hay varios tipos según su tamaño, es decir, en función de los grados que tenga:
Ángulo agudo. Es aquel que mide menos de 90° y más de 0 °.
Ángulo recto. Es aquel que mide 90° y sus lados son siempre perpendiculares entre sí.
Ángulo obtuso. Es aquel mayor que 90° pero menor que 180°.
Ángulo llano. Es aquel que mide 180°. Igual que si juntamos dos ángulos rectos.
https://www.youtube.com/watch?v=4pGyx2PrfgM ángulos happy learning
Ejemplos de ángulos en la vida cotidiana
En el cono del helado y en la separación de los siguientes dedos tenemos ángulos agudos, ya que su abertura es menor de 90º.
En la posición de los siguientes dedos en forma de L y en la esquina del corcho podemos observar los ángulos de 90°, rectos.
La apertura del abanico es mayor que 90° y menor que 180°, por lo cual tenemos un ángulo obtuso.
Y por último tenemos un brazo estirado formando un ángulo llano de 180°.
En el reloj podemos observar también los tipos de ángulos según la posición de las manecillas.
________________ ___________________ ____________________ ______________
Coloque que tipo de ángulo se forma en cada reloj según la posición de las manecillas.
Fecha máxima de entrega jueves 25 de marzo
Cuando envíen las evidencias al docente respectivo, se debe escribir en Asunto: Apellidos y nombres completos del estudiante, seguido del área y fecha de la actividad correspondiente.
Ejemplo… Asunto: Pérez Pepito Artes marzo 1-5
correos según el curso.
· 502actividades2021@gmail.com
